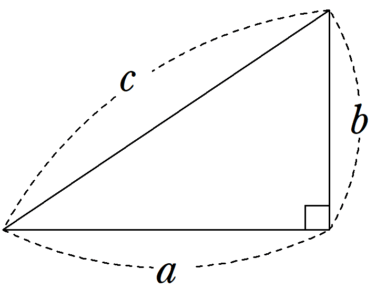
二等辺三角形は、2つの底角が等しい定理 二等辺三角形は、頂角の二等分線は底辺を垂直に2等分する定理 正三角形は、3辺が等しい三角形定義 正三角形は、3つの内角が等しく、すべて60°定理 直角三角形は、1つの角が直角である三角形 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。02 人教版八年级数学上册1331 等腰三角形的性质(第1课时 03 41认识三角形 04 三角形的面积 05 三角形内角和 06 三角形内角和

わかりやすい三角比と基本公式 Irohabook
三角形の定理 表
三角形の定理 表-二等辺三角形の4つの性質と4つの条件 二等辺三角形の角度の求め方と例題 対頂角、同位角、錯角の意味を分かりやすく解説 四角形の内角の和が360°であることの2通りの証明 多角形の内角の和の公式を3通りの方法で証明する 正多角形の内角と外角の大き左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club
三角形の面積 ・三角比を用いた三角形の面積公式を導く過程を考察 することができる。 数学的な見方や考え方 ・正弦定理・余弦定理の利用の仕方及び三角形の面積 の求め方について基礎的な知識を身に付けている。 知識・理解 観察・発表・課題内容資料説明資料0214 内容系統表(小学校算数〜中学校数学) 小 学 校 領域 1〜3年 領域 4〜6年 A 数と計算 数 ・1程度までの数 ① ・程度までの数 ②三角形 三平方の定理 正弦定理 余弦定理 メネラウスの定理・チェバの定理 多角形 円 方べきの定理 立体図形 面積と体積 平面図形の面積 立体図形の表面積 体積 ベクトル 初等代数
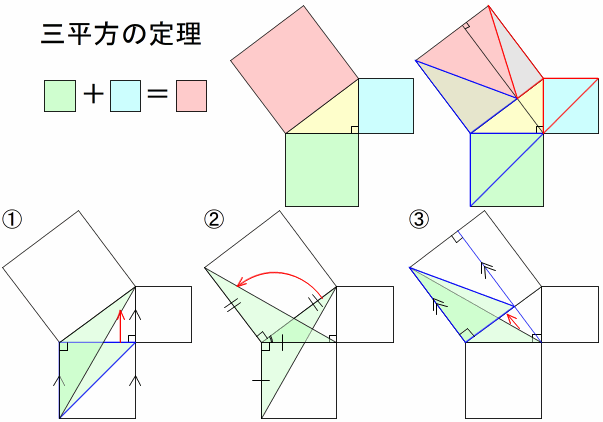
求三角函数角度对照表 : sin0=0sin30=05sin45= 二分之根号2sin60= 二分之根号3sin90=1cos0=1cos30= 二分之根号3cos45= 二分之根号2cos60=05cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3 供胆垛 三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b
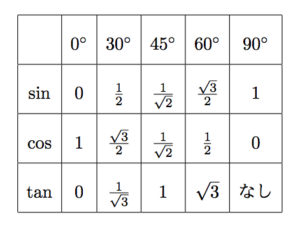
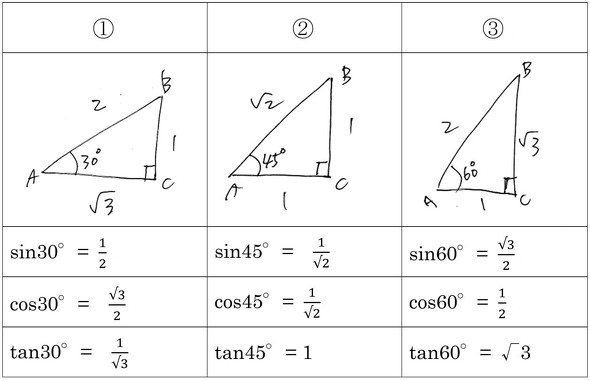
・正三角形(面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 直角三角形 ・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。・正方形,長方形の面積 ・角の大きさ 4年 ・図形の合同,多角形,正多角形, 円周率 ・角柱や円柱 ・三角形,平行四辺形,ひし形, 台形の面積 ・立体図形の体積 5年 ・縮図や拡大図 ・対称な図形 ・概形とおよその面積 ・円の面積 ・角柱及び円柱の体積直角三角形の中でsin サイン ・cos コサイン ・tan タンジェント の値を求められるようになろう 直角三角形の中で三角比を求めるために、以下のような直角三角形を書いて考える。 「三平方の定理」で、この2つの直角三角形の「辺の比」を覚えたと思う。




数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext
三角形,四角形,長方形, 正方形,直角三角形 2年 絵や図を用いた数量の表現 1年 表や棒グラフ 3年 円グラフ,帯グラフ 統計的な問題解決の方法 5年 測定値の平均 起こりうる場合 簡単な表やグラフ 2年しかし、 と を合わせてできる平行四辺形を考えると、平行四辺形1個の面積は2cm2となり、ピックの定理で求 行四辺形1個は2(cm22)。 問題2)辺の長さが 5 、 10 、 13である三角形の面積を求めよ。 勾股定理的公式 —— 在我国,把直角三角形的两直角边的平方和等于斜边的平方这一特性叫做勾股定理或勾股弦定理,又称毕达哥拉斯定理或毕氏定理(Pythagoras Theorem)数学公式中常写作a^2b^2=c^2 定义在任何一个直角三角形(RT )中,两条直角边的长度的平方和等于




1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2



数学史3 7 バビロニアの数学 三平方の定理 Fukusukeの数学めも
正三角形の 1 辺の長さを②とすると、 1 辺はその半分なので①となります。 残り 1 辺を三平方の定理を使って求めると、 三平方の定理 1 2 x 2 = 2 2 これを解いて、 x = 3 よって、その辺の比は、 1 2 3 となります。 ② 45 °, 45 °, 90 ° POINT:正方形の一个著名的例子是 345 三角形,由于 3 2 4 2 = 5 2 ,因此边长为3,4,5的三角形一定是直角三角形。 古埃及人不知道毕达哥拉斯定理,但他们知道 345 三角形。在建造金字塔的时候,他们使用的就是长度为3,4,5的打结绳来测量完美直角。初等幾何学 における ピタゴラスの定理 (ピタゴラスのていり、 英 Pythagorean theorem )は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は が成り立つという 等式 の形で述べられる 。




三平方の定理を教えてください Clear




三角比 高校物理の備忘録
三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
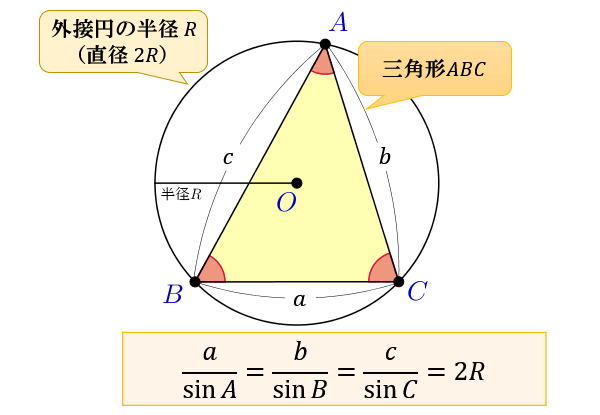
21 四角すいの表面積 右図のように,一辺の長さが 2 cm である正方形を底面とする正四角すい tabcd があり, ta =tb =tc =td = 3 cm です。 このとき,次の問いに答えなさい。 (1) (ア) 正四角すい tabcd の表面積を求めなさい。 以下略正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出"在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍",即a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。 三角比・三角関数の公式一覧。正弦・余弦・加法定理など sinθ cosθ tanθ の覚え方・弧度法・三角比の表 2倍角の公式・半角の公式とその証明。二等辺三角形で分かる2



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三角比の値の求め方 数学苦手な人に向けて基本をイチから解説していくぞ 数スタ
三平方の定理 225°,\ 675°の三角比は数II}で半角の公式を学習すると割と容易に求められる よって,\ 15°,\ 75°の三角比と同じく参考程度の問題である まず,\ 各辺の長さをすべて求める\ 本問の2重根号ははずせない このため,\ 有理化を含めた式変形が厄介第一个三角函数表是由 喜帕恰斯 编制而成的,他被后世称为"三角学之父"。 苏美尔 天文学家引入了角度测量,将一个圆分割为360度。三角形与三角学三角函数 三角函数 到目前为止,我们已经知道了三角形_角_之间的关系(例如,角的总和为180°)及_边_之间的关系(例如,毕达哥拉斯定理),但是没有任何东西将角和边的大小 关联 起来。 举个例,如果我们知道一个三角形的三条边,如何




弧度法とは 度数法との違いと表 求め方 理系ラボ




三平方の定理 覚えておきたい基本公式を解説 数スタ
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し题1: 关于三角形所有定理及概念数学科目 15 定理 三角形两边的和大于第三边 16 推论 三角形两边的差小于第三边 17 三角形内角和定理 三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角 勾股定理是建立在直角三角形上的边的关系余弦定理是可以用在非直角三角形上的边与角度的关系 勾股定理和三角函数算出来不一样 : 你确定?a30°,角b60°,角c90°,这个角度怎么可能ac长为4,bc长度为3?你这个角度的话三条边比例为12√ ̄3题都是错的




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ




三角関数の知識 やさしい電気回路
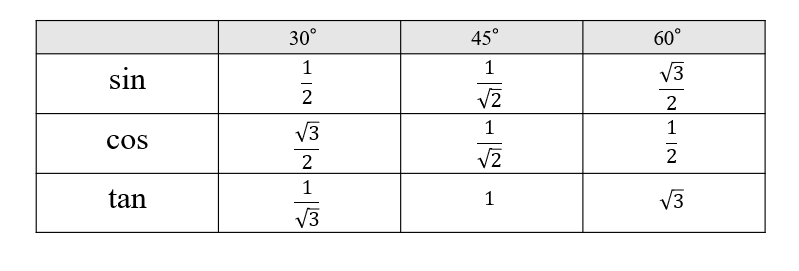
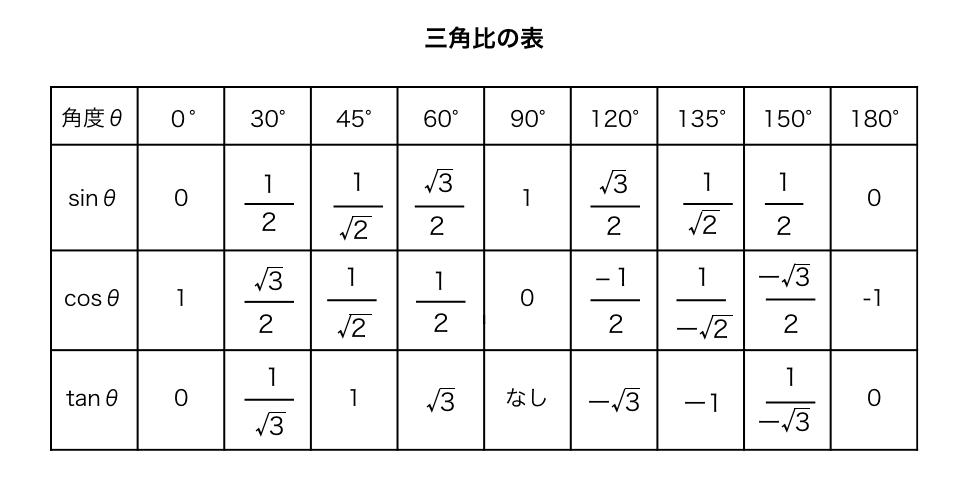
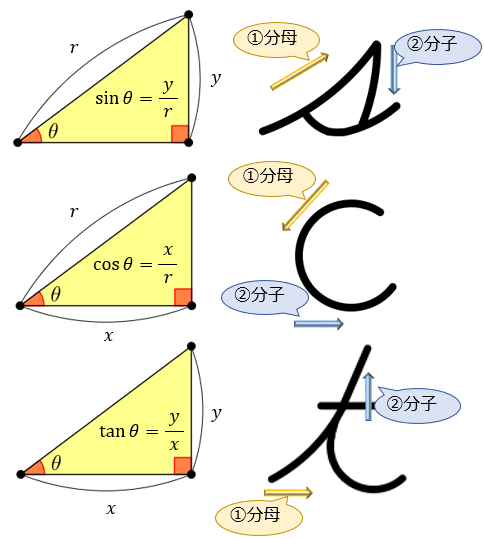
直角三角形での三角比の覚え方とは、 直角が右下に来るように直角三角形を動かした後 、 筆記体「s」を当てはめることでsinを求め、 筆記体「c」を当てはめることでcosを求め、 筆記体「t」を当てはめることでtanを求める方法です ≪三角比の表≫ θ ( ) sin容は大体,正弦定理,余弦定理,三角形の解法, * (Yamaguti Kiyosi) 広島大学名巻教授 三角形の面積および空間図形の計量的性質で ある。「数学II 」で三角関数,加法定理を学習 する。「数学B」で複素数を2次方程式の解と の関連において学習する。 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に




3 4 5の三角形で 本当に直角ができる Note Board



三角関数とは コトバンク
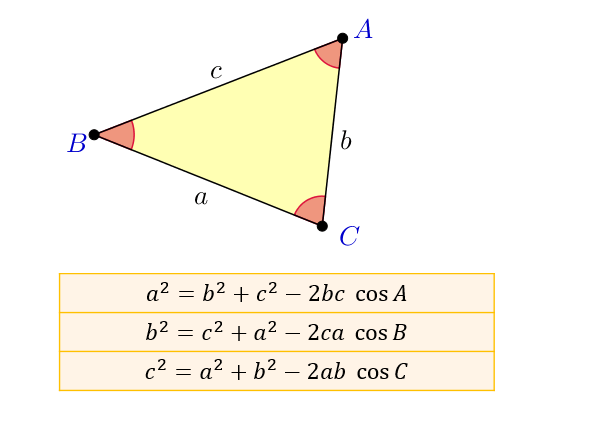
使用した定理・公式 本題の計算の前に、各辺の長さが1cmの正三角形が半径 r (cm)の球上にあるとして、その球の半径に対して正三角形の面積がどのように変化するかを計算してみました*4 GeoGebraで描いてみました。 半径 r が小さいと球を覆うような三角形と余弦定理,欧氏 平面几何 学基本 定理 。 余弦定理是描述 三角形 中三边长度与一个角的 余弦 值关系的数学定理,是 勾股定理 在一般三角形情形下的推广,勾股定理是余弦定理的特例。



3




三角関数の知識 やさしい電気回路




三角関数 改訂第2版 ニュートンプレス




三角関数の公式の一覧 Wikipedia



単位円とは 1分でわかる意味 覚え方 表 Sin Tanとの関係



2




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club
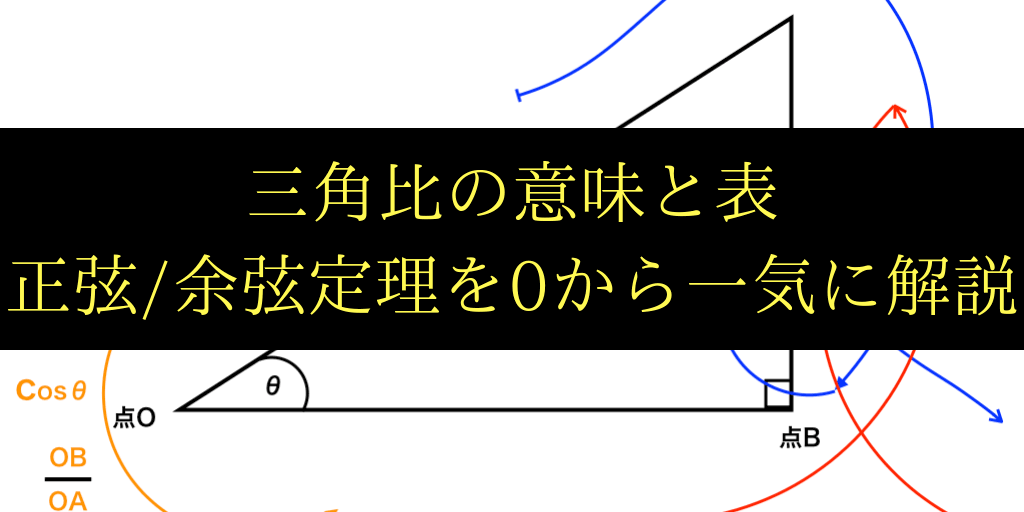



三角比の表と面積公式 正弦定理 余弦定理を一記事で解説
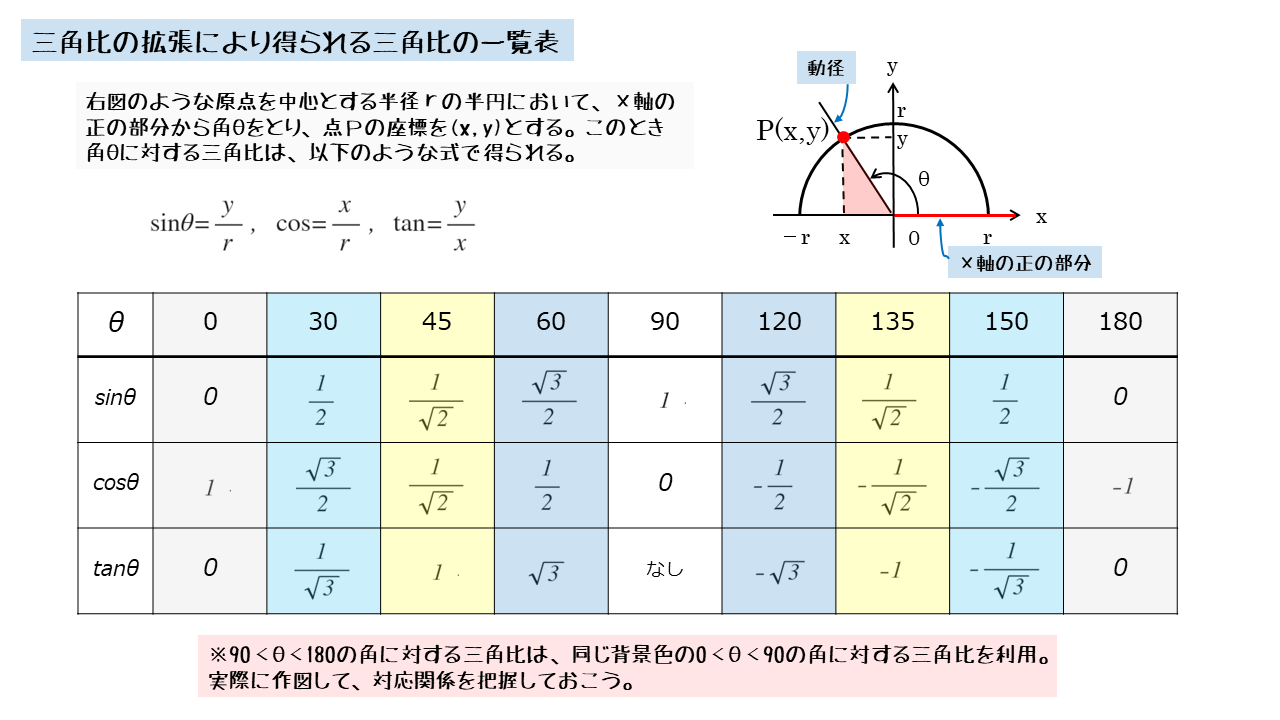



図形と計量 三角比の拡張について 日々是鍛錬 ひびこれたんれん




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月




壁紙 押入れ トップ 100 三 平方 の 定理 表
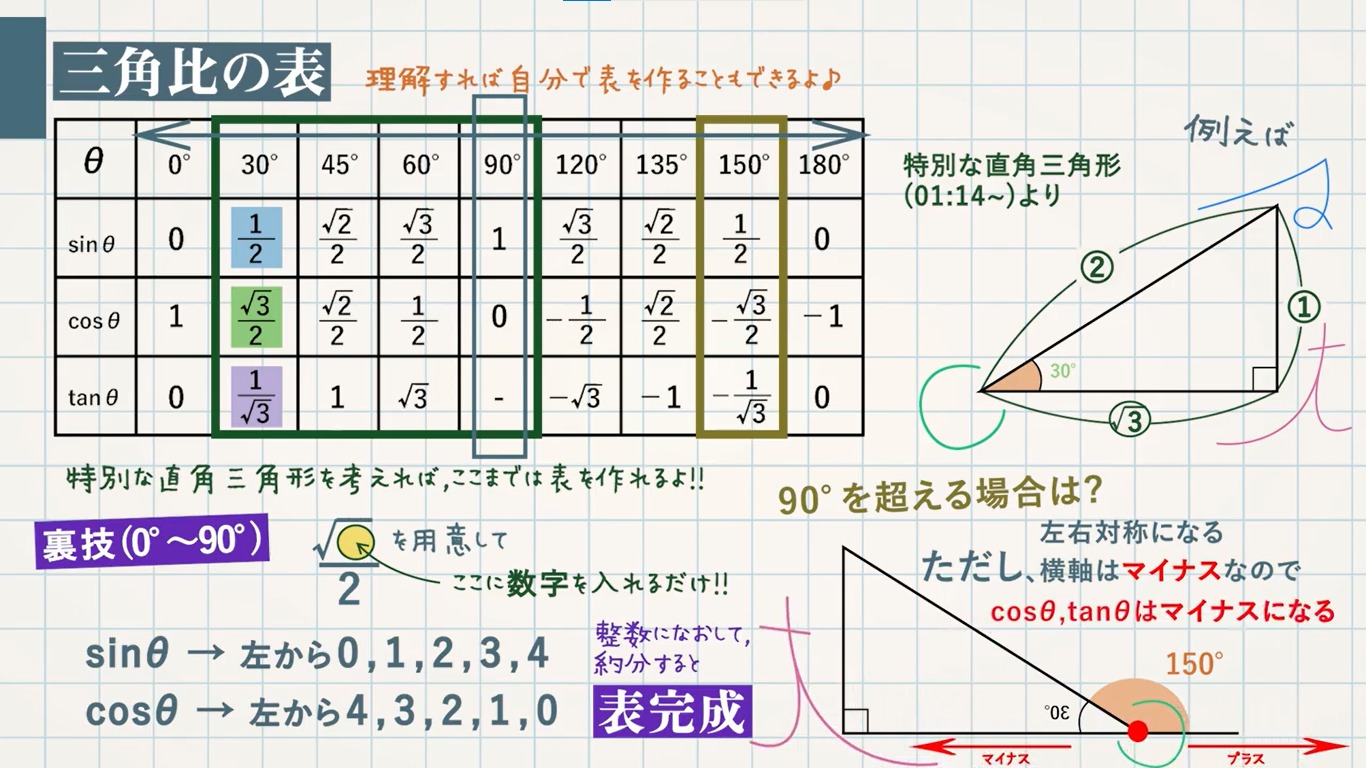



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
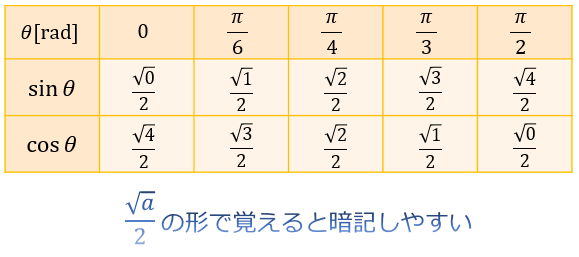



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
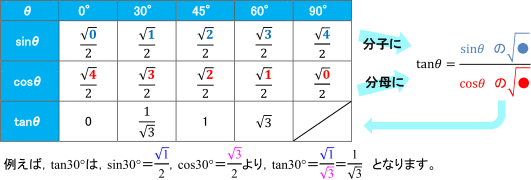



Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座



三平方の定理




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ
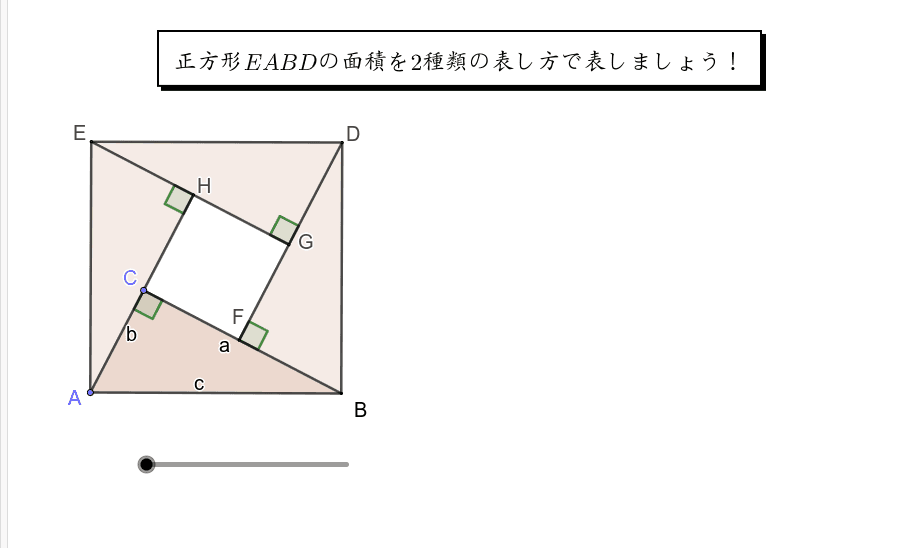



三平方の定理の証明 Geogebra




三角比の表を見て三角形の角度を求める問題 数学i By ふぇるまー マナペディア
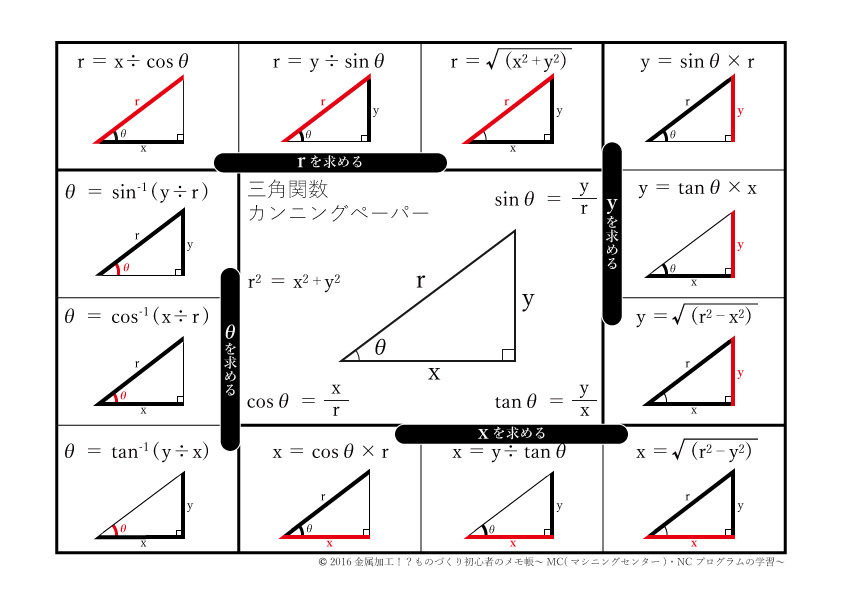



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



3




わかりやすい三角比と基本公式 Irohabook
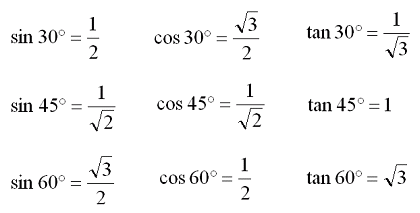



三角比 基本的な直角三角形の三角比 大人が学び直す数学



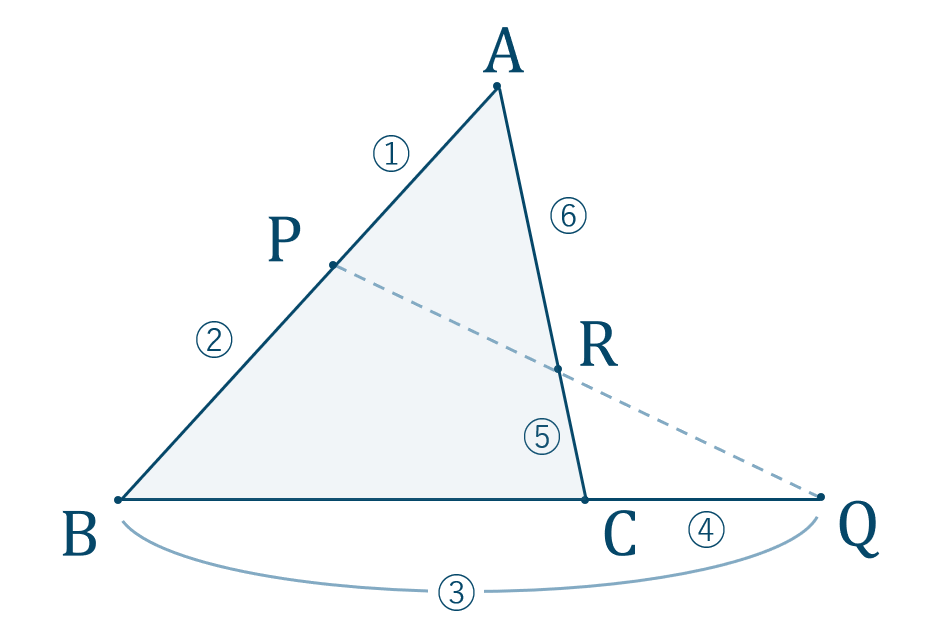
角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



正弦定理とは 公式や余弦定理との使い分けをわかりやすく解説 Studyplus スタディプラス




高校数学 数 79 三角比 暗記編 Youtube




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
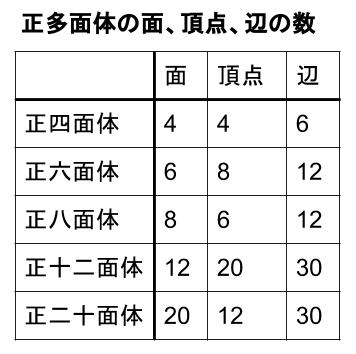



中学数学 正多面体 中学数学の無料オンライン学習サイトchu Su




三角法とは コトバンク




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
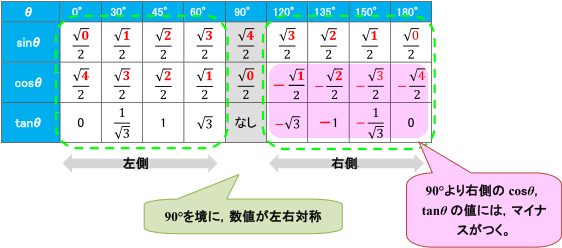



Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット




都立入試数学 三平方の定理を使わなくても解けるか 都立に入る




細かい質問ですが この問題でsin1 8の三角比の値を求めるのに Clear




オイラーの多面体定理を解説 簡単な証明付きで即理解 高校生向け受験応援メディア 受験のミカタ



三角比の相互関係とその使い方 高校数学の知識庫




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 相似を利用した問題 問11の 2 を教えてください Clear




三角法とは コトバンク




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
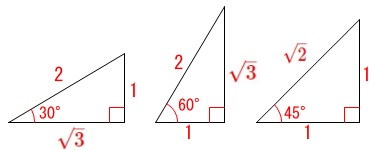



三角比 図形と計量 の要点




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ



三角比は丸暗記ですか この表は丸暗記するのでしょうか 暗記する Yahoo 知恵袋




高校数学 数 76 三角比 基本編 Youtube




わかりやすい三角比と基本公式 Irohabook




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三角関数の知識 やさしい電気回路




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2
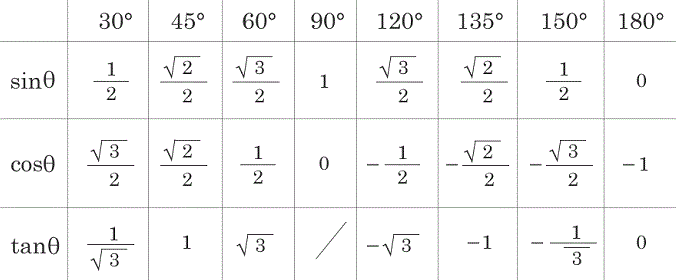



三角比 三角関数基本公式 優技録



3 4 5の三角形で 本当に直角ができる Note Board




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学



三角関数の公式 Sin Cos Tan と覚え方



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学



1




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




わかりやすい三角比と基本公式 Irohabook



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三角比を用いた計算問題をマスターしよう スタディクラブ情報局




三角関数 Sin Cos Tanの表について 写真の表って全部覚える必要ありま 数学 教えて Goo



この表って2つあるんですか 三角関数です どちらも同じですよ 1 2を Yahoo 知恵袋




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三角比の等式や不等式を満たす角 怜悧玲瓏 高校数学を天空から俯瞰する




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




応用 15度の三角比 なかけんの数学ノート



3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




余弦定理の覚え方 語呂合わせやイメージで暗記しよう 数学の面白いこと 役に立つことをまとめたサイト



3



2



三角比の表 について どうして75度と90度がないんですか 90 Yahoo 知恵袋



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
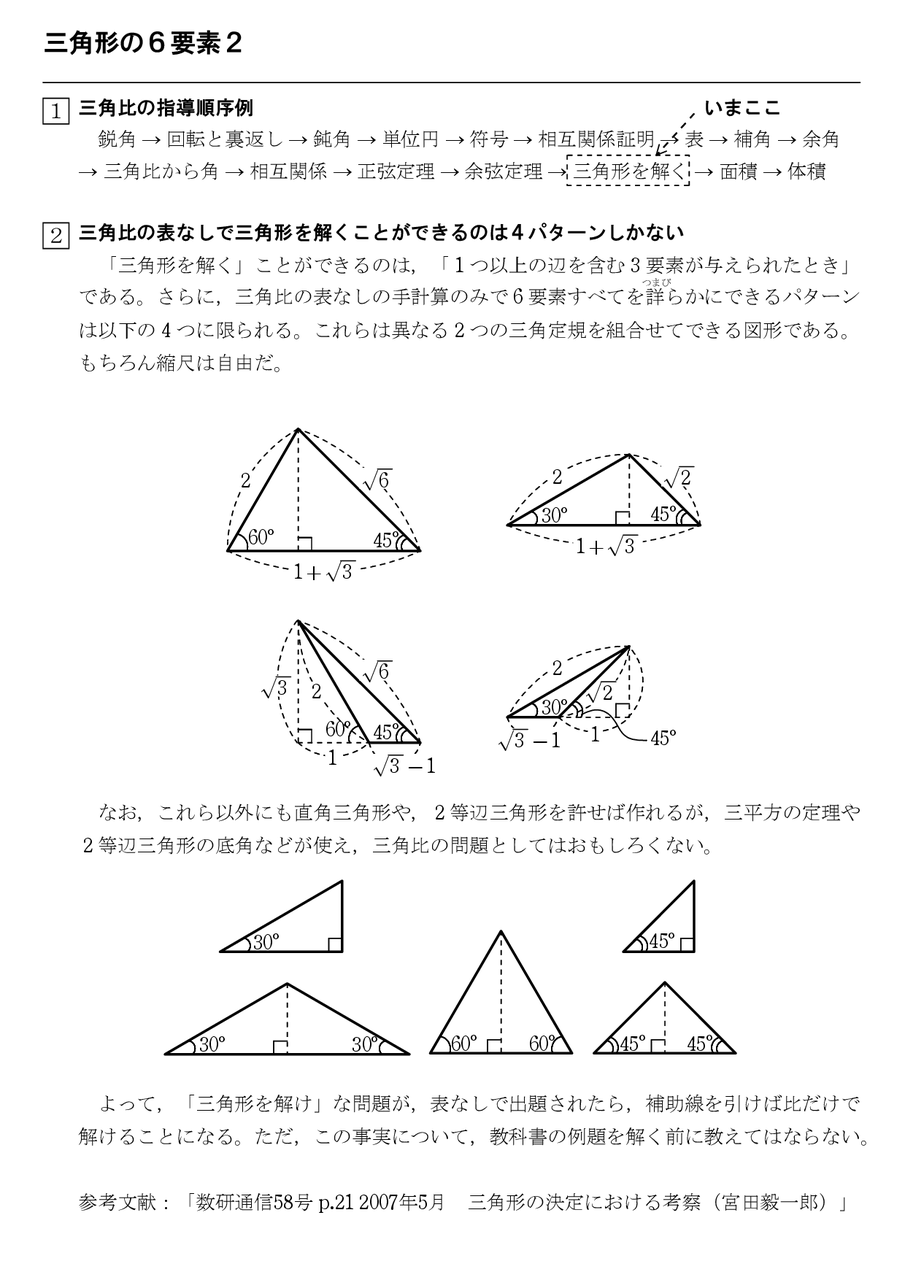



三角形の6要素2 怜悧玲瓏 高校数学を天空から俯瞰する




1分で覚えて一生忘れない三角比の覚え方 動画5分 Youtube




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
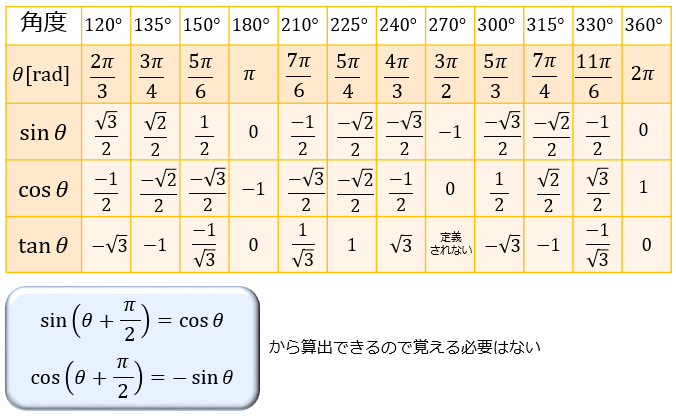



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
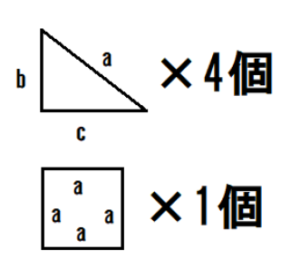



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会



0 件のコメント:
コメントを投稿