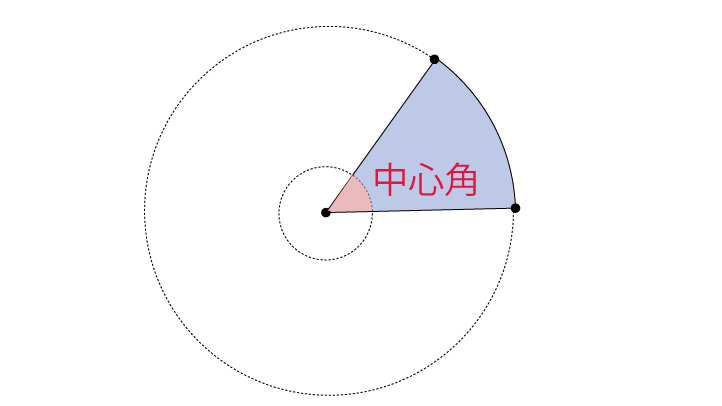
本頁面最後修訂於年6月7日 (星期日) 0221。 本站的全部文字在創用CC 姓名標示相同方式分享 30協議 之條款下提供,附加條款亦可能應用。 (請參閱使用條款) Wikipedia®和維基百科標誌是維基媒體基金會的註冊商標;維基™是維基媒體基金會的商標。 維基媒體基金會是按美國國內稅收法501(c)(3採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ
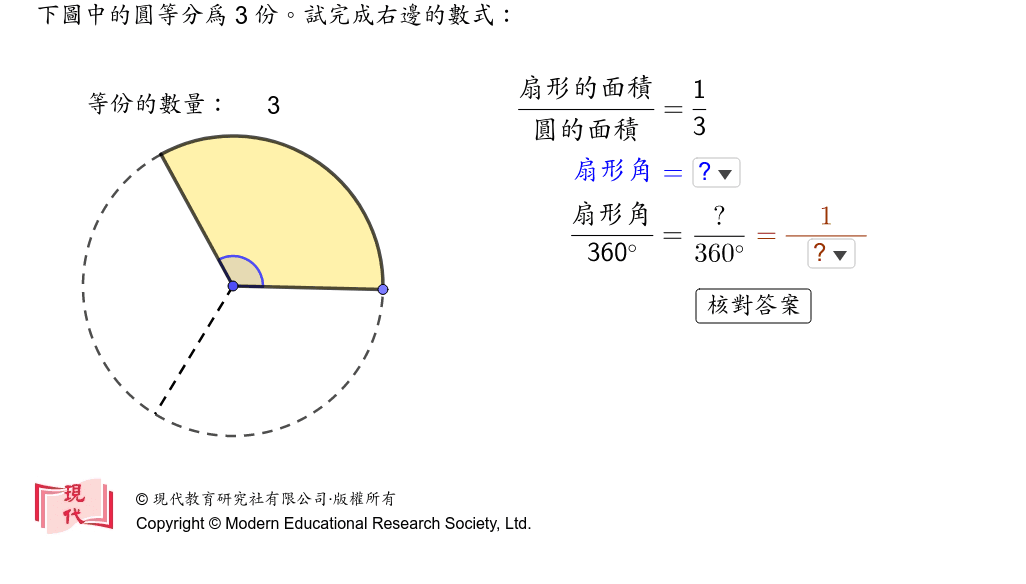
扇形面積公式 Geogebra
扇形の面積 公式
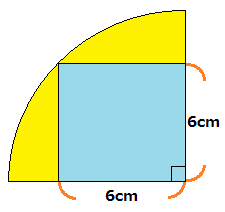
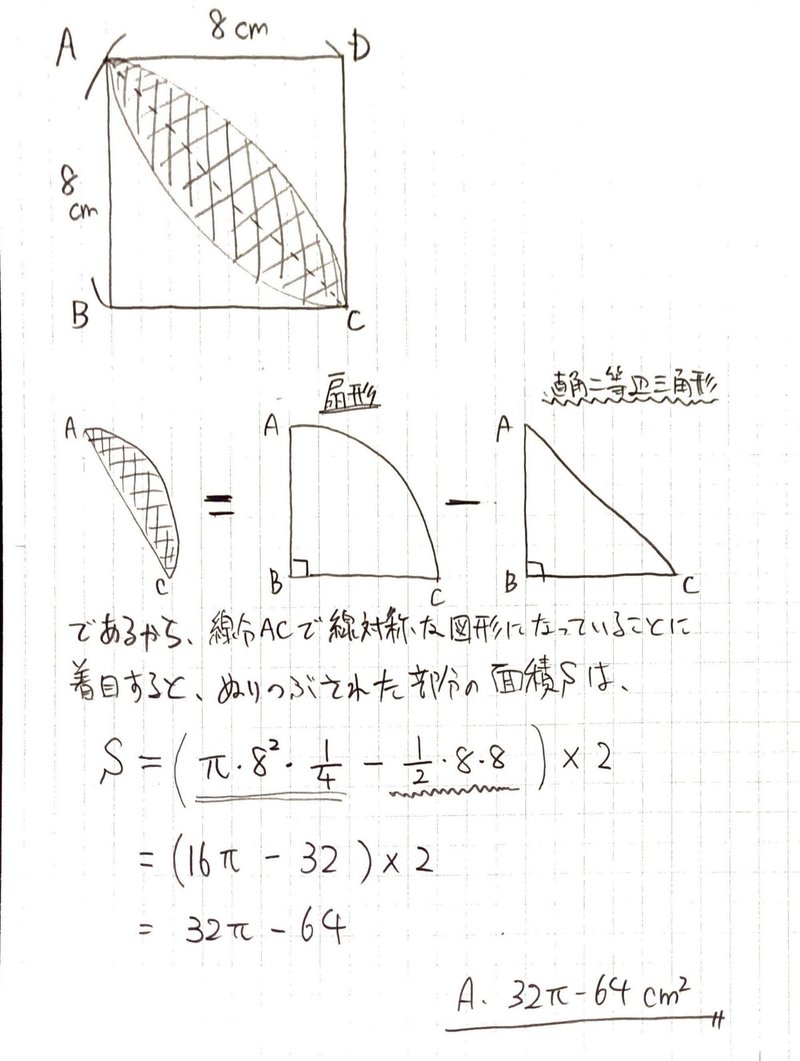
扇形の面積 公式-求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! (扇形の面積)=π(10) 2扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r,跟角度要我們求扇形的弧長或面積,我們就可以輕鬆的套公式把它算出來了
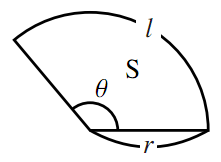



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
主題二 弧長與扇形面積 扇形的弧長與面積公式: 若圓半徑為 r,扇形 COD 的圓心角 ∠COD=θ(弧度),2π, ≤ θ 0 ≤ 如下圖所示,令扇形的弧長為 s,面積為 A,則:円の接線、おうぎ形の作図の練習や、円周率(π)を用いて円とおうぎ形の弧の長さや面積を求める練習、また、おうぎ形の中心角の求め方などを練習できる問題プリントです。 円とおうぎ形(1) 答え 円とおうぎ形(2) 答え 円とおうぎ形(3) 答え 扇形とは? 面積・中心角・半径・弧の長さの公式と求め方 21年2月19日 この記事では「扇形(おうぎ形)」について、面積の公式や半径・中心角、この長さの求め方をできるだけ簡単に解説していきます。 また、弧度法(ラジアン)で解く計算問題など
扇形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐公式 以下是扇形麵積的計算公式: 其中: A =扇區的麵積 π= r =圓的半徑 θ=以度為單位的中心角・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。 ・扇形の面積 半径と中心角から扇形の面積、円弧の長さ、弦の長さを計算します。
極方程式の面積公式の使用例1 まずは一番簡単な例である円の面積を求めてみます。 半径 R R R の円の方程式は極座標では r = R r=R r = R と表されます。 よって,半径 R R R の円の面積は, ∫ 0 2 π 1 2 R 2 d θ = π R 2 \displaystyle\int_0^{2\pi}\dfrac{1}{2}R^2d\theta=\pi R^2 ∫三角形DEFの面積は三角形ABCの面積の何倍ですか。 → 解答 問題4 たて5cm、よこ9cmの長方形の紙が4まい、図のように重なっています。ア、イ、ウの部分の面積はともに6c㎡、エの部分の面積は10c㎡、全体の面積は119c㎡です。初等幾何学における弓形(ゆみがた、英 circular segment (記号 ⌓ )は、円板から割線または弦によって残りの部分から「切り取られる」部分を言う。 より厳密には、円の劣弧(中心角が180°未満の弧)とその円弧の両端点を結ぶ弦で囲まれた二次元の領域を弓形という。



色々な扇形の面積 その1 名古屋市北区の学習塾は思考力を育む 泰成スクール




扇形面積公式弧長14 Zilhc
同様に扇形の 面積 S も中心角の大きさに比例する。 半径 r の円板の面積は πr2 であるので、中心角が θ のときC 扇形弧長S=rθ d 扇形面積A=1 2 r2θ=1 2 rS (2)三角函數的定義 正弦函數sinA=∠ 的對邊 斜邊 餘弦函數cosA=∠ 的鄰邊 斜邊 正切函數tanA=∠ 的對邊 ∠ 的鄰邊 餘切函數cotA=∠ 的鄰邊 ∠ 的對邊 正割函數secA= 斜邊 ∠ 的鄰邊 餘割函數cscA= 斜邊 ∠ 的對邊 (3)三角函數弓形・扇形面積の計算式 ①扇形の面積(Fun) 扇OCD の面積(F)は θ θ 2π 2= 2 r2・・・・F ②弓形の面積(Bow) 三角形OCD の面積(S)は 2×三角形OCB OB×BC 2 θ θ Cos( 2 )×sin( 2 ) =2× 2 θ θ =Cos( 2 )×sin( 2 )・・・・S したがって弓形OCD の面積(B)はF
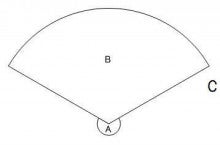



中心角が分からない扇形の面積の求め方の裏ワザ 爽のつぼやき



物理のための数学 図のbを含む扇形の面積の求め方を教えてくださいますでしょう Yahoo 知恵袋
$$扇形の弧の長さ=直径 \times 円周率\times \frac{中心角}{360}$$ 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積問題では扇形の面積が を含む値で示されているので、解答もそれに準じた形を取りましょう。 16 X 出典文献 円周率を314として計算する場合は、1 x 314を計算すると答えは3768 cm 2 になります。 Step3 側面積(扇形の面積)をだす! 中心角が求まったね?? 最後に、円錐の側面の「扇形の面積」と計算してあげよう。 扇形の面積は、 (半径)×(半径)×(円周率)×(中心角)÷360だったよね?? だから、例題の側面の扇形の面積は、 10×10×π×108/360
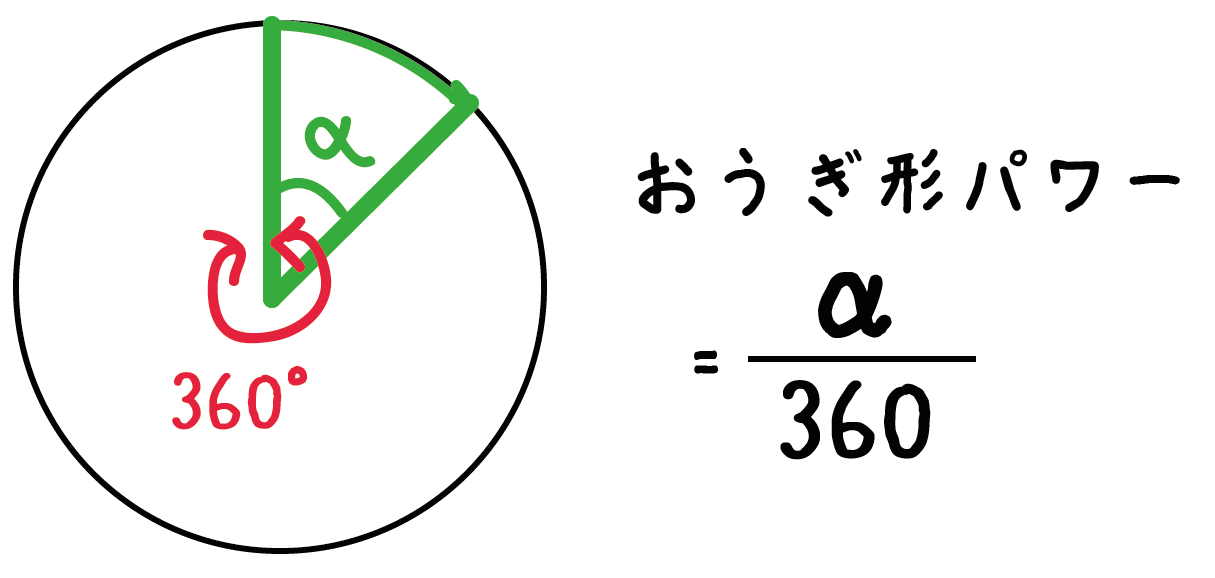



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張
側面積 = 36π × 4π 12π = 12π 側面積 = 36 π × 4 π 12 π = 12 π 最後に、円錐の表面積は、底面積と側面積を足し合わせて S = 4π 12π = 16π S = 4 π 12 π = 16 π となります。 ※ 補足 ちなみに、扇形の面積同様、扇形の中心角も弧の長さに比例します。 よって扇形の面積 = 半径$×$半径$×π×\displaystyle\frac{中心角}{360°}$ この2つの式を見比べたとき、「似ている」と思わないでしょうか。そこで、扇形の弧の長さを出す公式に対して、両辺に「半径$×\displaystyle\frac{1}{2}$」を掛けましょう。扇形還與三角形有相似之處,上述簡化的 面積公式 亦可看成:1/2×弧長×半徑,與三角形面積:1/2×底×高相似。 公式: S扇=(lR)/2 (l為扇形弧長) = (1/2)θR 2 (θ為以弧度表示的圓心角)



扇形の面積が苦手 を克服する方法 中学受験ナビ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
弧度を使って弧の長さと面積を求める このテキストでは、弧度を使って弧の長さと面積を求める方法を解説しています。 半径がrで中心角がθの扇の弧の長さをl、面積をSとしましょう。 扇の弧の長さ ここで思い出してください。円の弧の長さは まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の弧度法において扇形の面積が 1 2 r 2 θ \dfrac{1}{2}r^2\theta 2 1 r 2 θ になることを証明します。 証明 度数法では, 半径 r r r ,中心角 A ∘ A^{\circ} A ∘ の扇型の面積は π r 2 × A 360 \pi r^2\times\dfrac{A}{360} π r 2 × 360 A であった。




中学数学の問題か 扇形の面積




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなるJw_cad その他の〔 測定 〕コマンドの「面積測定」を行うとき、図形に丸面取り処理などが施されている図形の面積を測定するときに使うのが「(弧 指定」ボタンです。 円弧を含む面積測定の使い方 「 測定 」コマンドを実行し、コントロールバーの「面積測定」ボタンを 左クリック します。S63 圓周率、圓周長、圓面積、扇形面積:用分割說明圓面積公式。求扇形弧長與面積。知道以下三個比相等:(1)圓心角:360;(2)扇形弧長:圓周長;(3)扇形面積:圓面積,但應用問題只處理用(1)求弧長或面積。 學習表現: sⅢ2 認識圓周率的意義



3




ラブリー扇形 弧の長さ 公式 最高のカラーリングのアイデア
扇形のまわりの長さは、 扇形の弧の長さ+半径×2 で求められます。 この扇形の弧の長さ=18×314× 1 ° 360 ° =14(cm) よって、求める扇形のまわりの長さは 14+9×2=3684(cm) 答え 3684㎝ ~平面図形の面積・まわりの長さを求める公式まとめおうぎ形の面積の公式と求め方 教科書には扇形の面積や弧の長さを求める公式があります。 半径を \,r\, ,中心角 \,a^\circ\, として、 扇形の弧の長さ \,\ell\, と扇形の面積 \,S\, の公式は、 \color {red} { \displaystyle \ell=2\pi r \times \frac {a} {360}\\ \displaystyle S=\pi r^2 扇形の面積の公式 まずは公式を見てもらいましょう。 この通り、円の面積をまず出して、円を360分割し、中心角分を集めてます。 弧の長さを計算するときと同じですね。 つまり、弧の長さを出すことが出来たなら面積も出せるということです。 計算のコツ




扇形 の 面積 の 求め 方 小学生 かわいいドラえもん



Spi M54e217p7lcis9d Com Category E5 9b E5 81 Ae E9 9d E7 8d
影の部分の面積、周の長さ(4)の解説 面積を求めるには、 おうぎ形から半円を引いてあげればOKですね。 このとき、半円の半径は6㎝になっていることにも注意です。 周の長さは、以下の3つのパーツ(赤、青、緑)を合わせれば求めることができます。扇形周長與面積 6年級數學(Grade 6 Math Fanshaped Area)




円 扇形 の面積 周や弧の長さの公式 数学fun
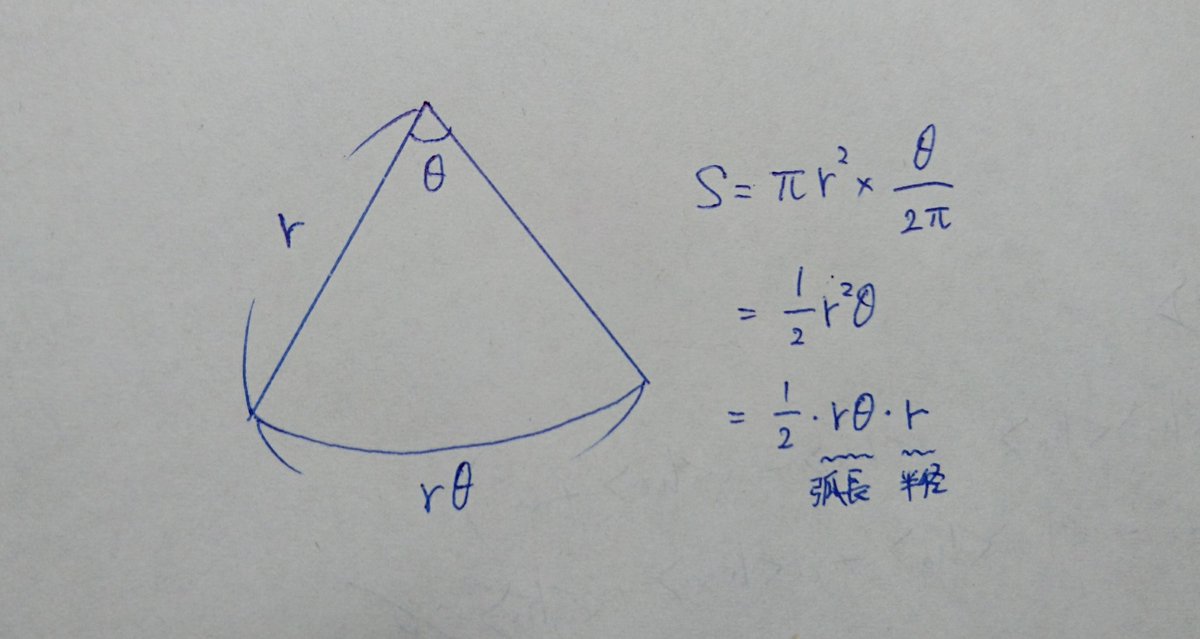



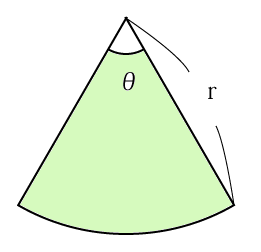
تويتر ヨビノリやす على تويتر センターのラジアンで思い出したんだけど 扇形の面積を求めるのに 扇形を三角形だと思い込んで 底辺 高さ 2 のように 弧長 半径 2 とすれば求められるのってみんな知ってる話 T Co Rgnzj006w3




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw



1




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



扇形の面積の解答と解説 多目的ルーム 楽天ブログ




極方程式の面積 扇形積分 おいしい数学



身近な数学 楕円の扇形 ケネディの7
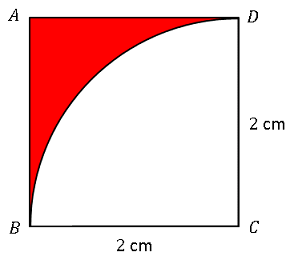



扇形の弧の長さと面積




円弧面積の計算式




扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




扇形の弧の長さと面積 計算ドリル 問題集 数学fun



他の解き方ないんですか Katsuya Saito Note
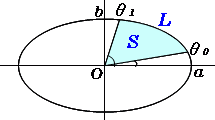



楕円扇形の面積 高精度計算サイト




05年 平成17年 10月から06年 平成18年 9月までの問題
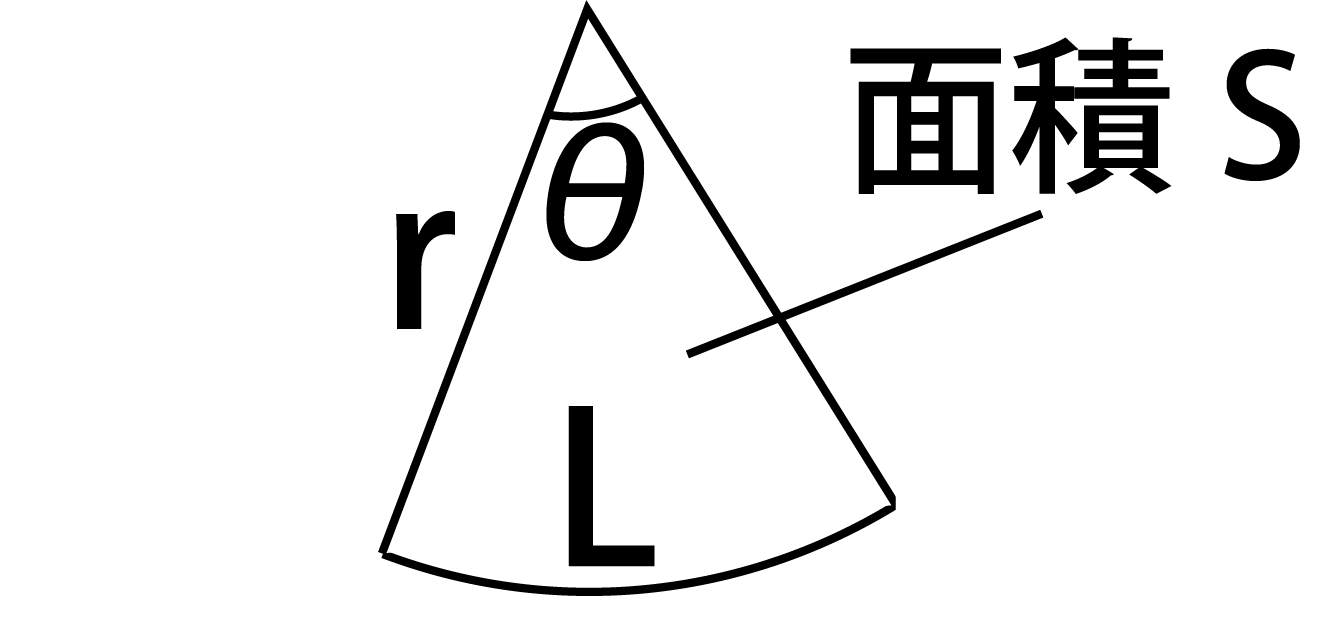



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




おうぎ形の面積 弧の長さ 数学ノート




この扇形の面積の途中式教えてください この扇形の面積の途中式教え 中学校 教えて Goo
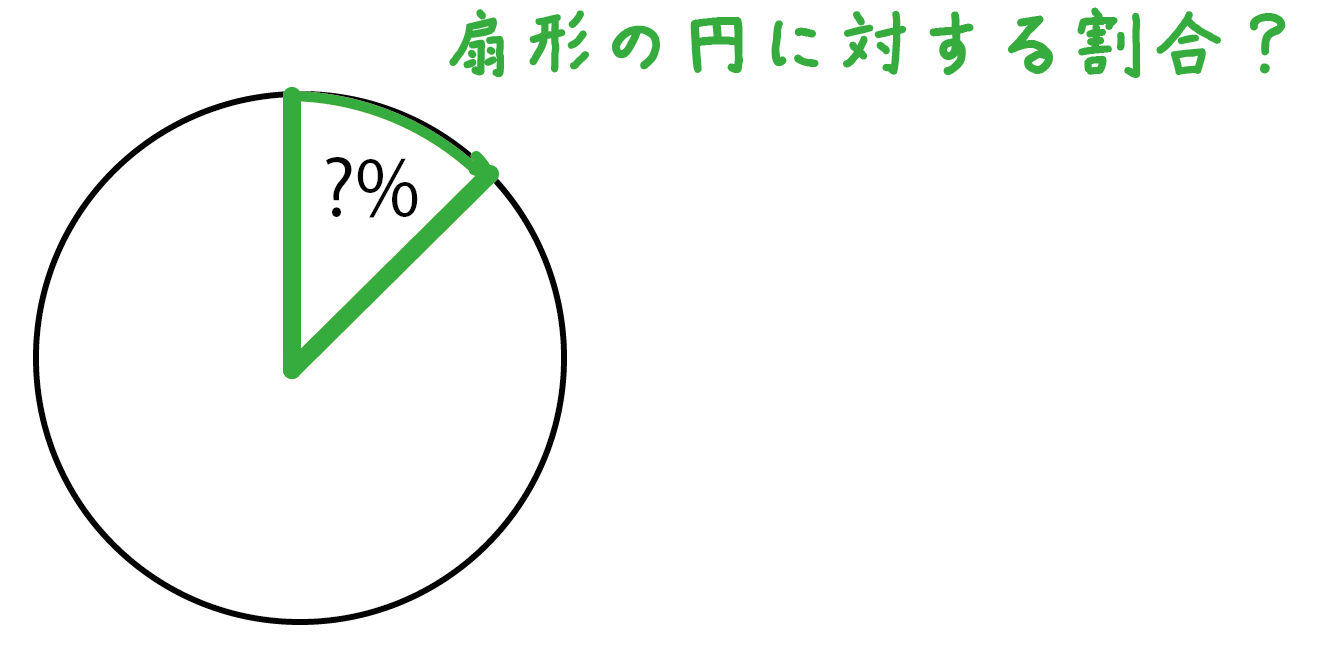



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




扇形面積公式 Geogebra




扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg




なぜ扇形の面積にするという考えになるのですか 解説を見ても分かりませんでした Clear
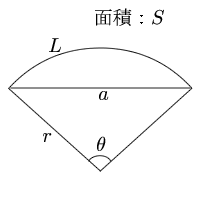



扇形 面積の計算 計算サイト




扇形の面積の求め方 公式と計算例
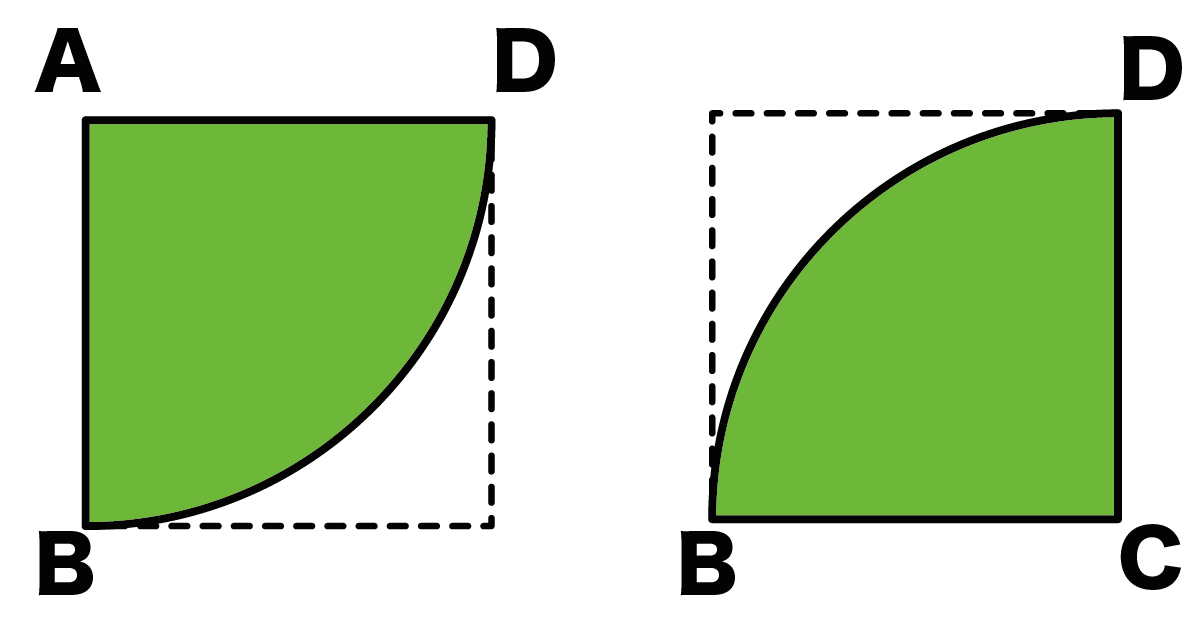



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
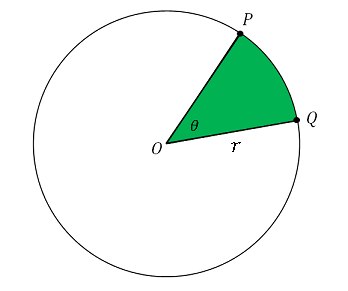



扇形の弧の長さと面積




数学ii 三角関数 1 3 扇形の弧の長さと面積 Youtube




扇形の面積の求め方 公式と計算例




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー
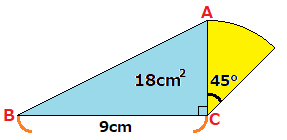



三角形と扇形の面積 多目的ルーム 楽天ブログ



扇形の面積 三角形の面積について



この円錐での扇形の面積って何m になりますか 円周角の求め方 Yahoo 知恵袋




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau



扇形の面積 Geogebra



写真の問題の解答には面積差 ア イ 扇形の面積 長方形の面積となっています Yahoo 知恵袋




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




色のついた部分の面積の求め方を教えてください Clear




なぜ扇形の面積にするという考えになるのですか 解説を見ても分かりませんでした Clear



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
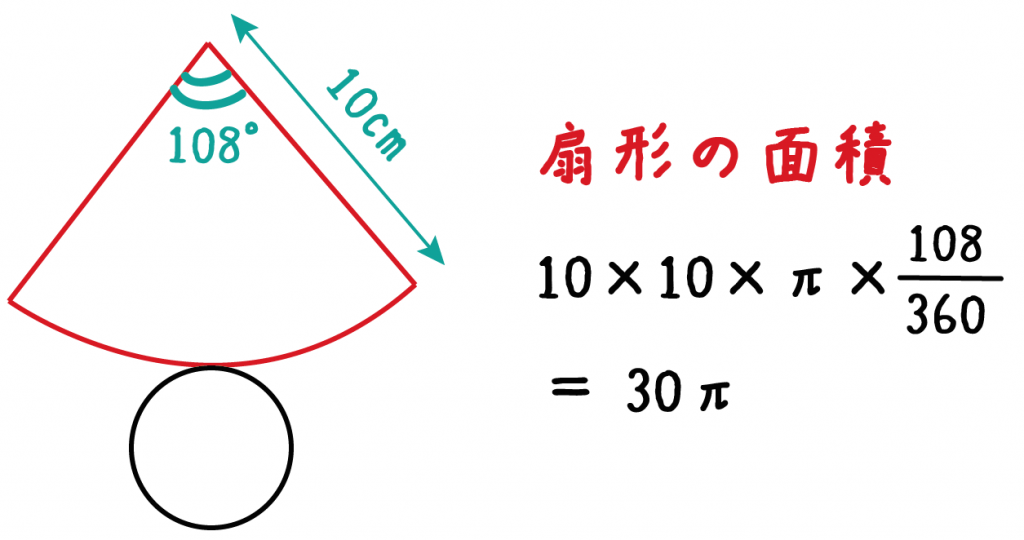



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
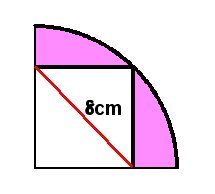



扇形と正方形



円と扇形 中学受験ー算数解き方ポータル




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




2 の三角形の断面と下の半円の面積は求められるのですが扇形の面積が求められません Clear
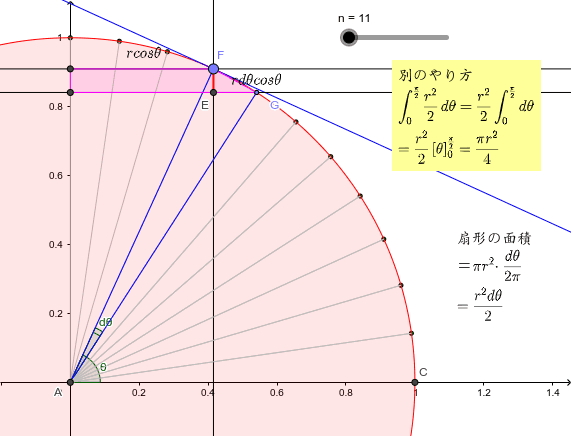



円の面積2 Geogebra




扇形の面積の求め方を教えてください Clear




扇形 Wikipedia




標準 おうぎ形と正方形の面積 なかけんの数学ノート




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube
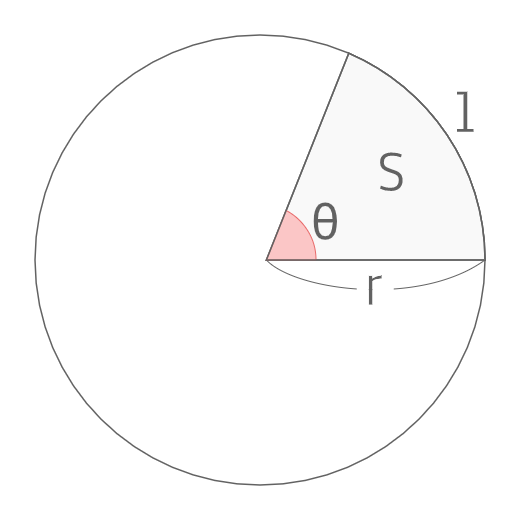



高校数学 扇形の弧の長さと面積 の公式とその証明 Enggy
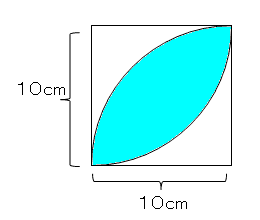



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に
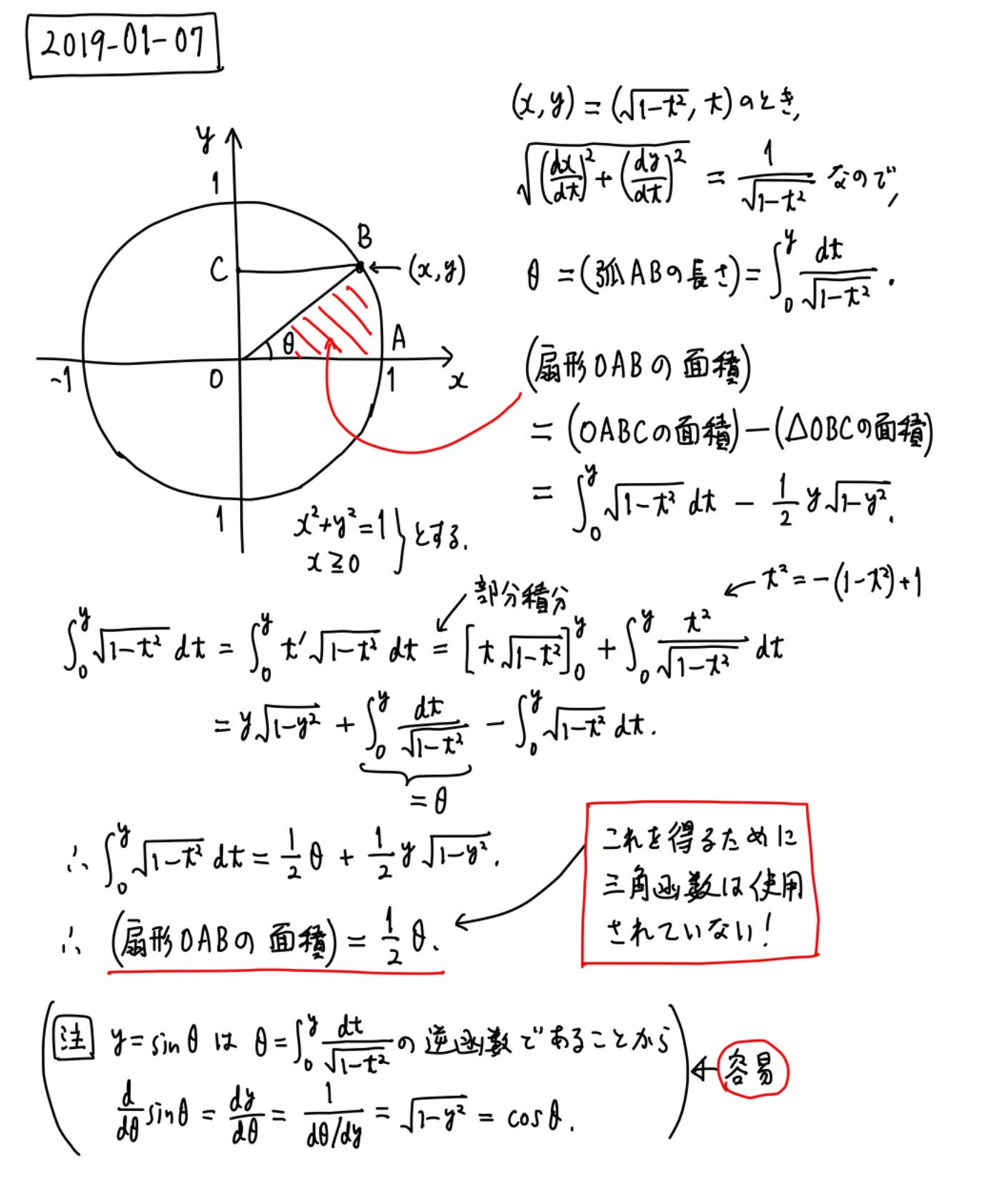



Uzivatel 黒木玄 Gen Kuroki Na Twitteru 数楽 訂正 誤 扇形oabc 正 扇形oab ポイント1 角度 弧abの長さをdt 1 T の積分で表示 ポイント2 扇形の面積を 1 T Dtの積分で表示 ポイント3 それらが部分積分で繋がる 訂正版解説画像 T




50 扇 面積 求め方
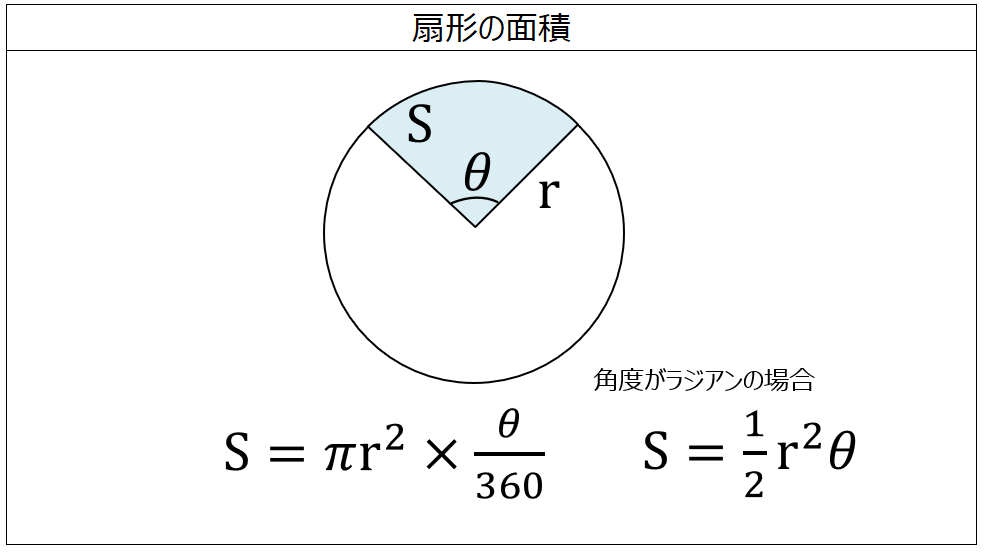



扇形の面積 製品設計知識




極方程式の面積 扇形積分 おいしい数学
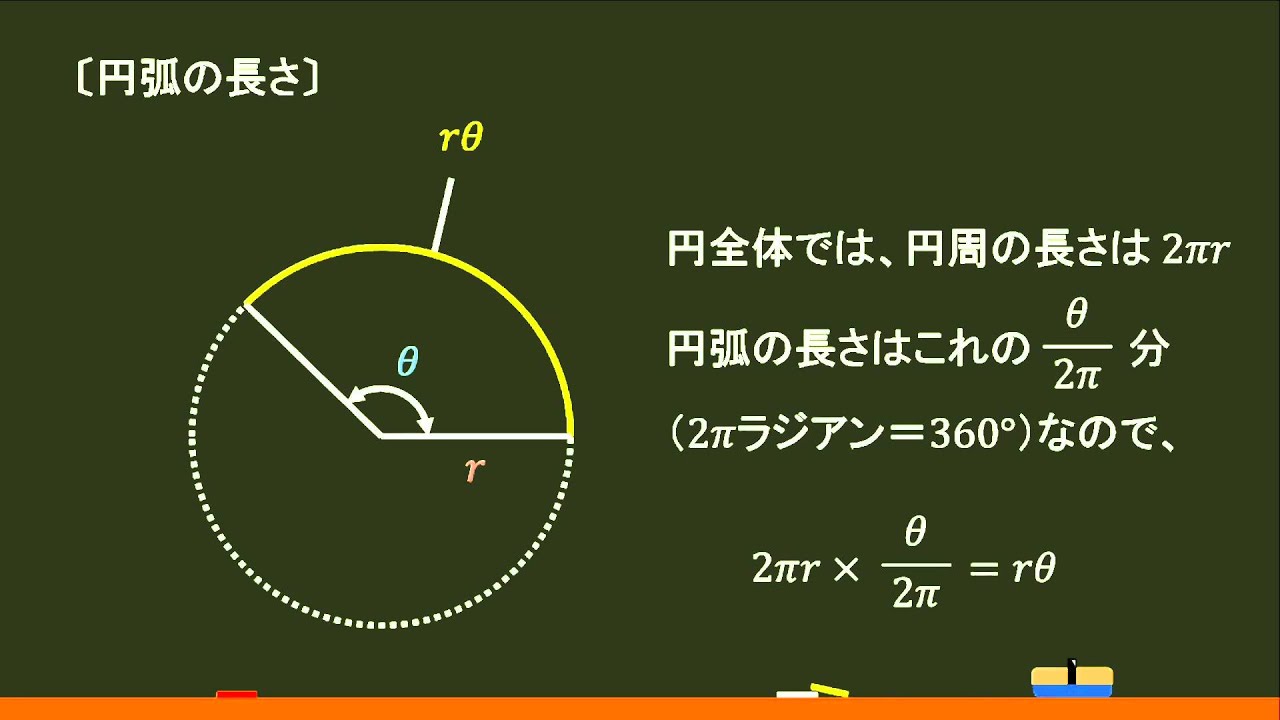



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube



扇形の面積と公式 面積計算機




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題
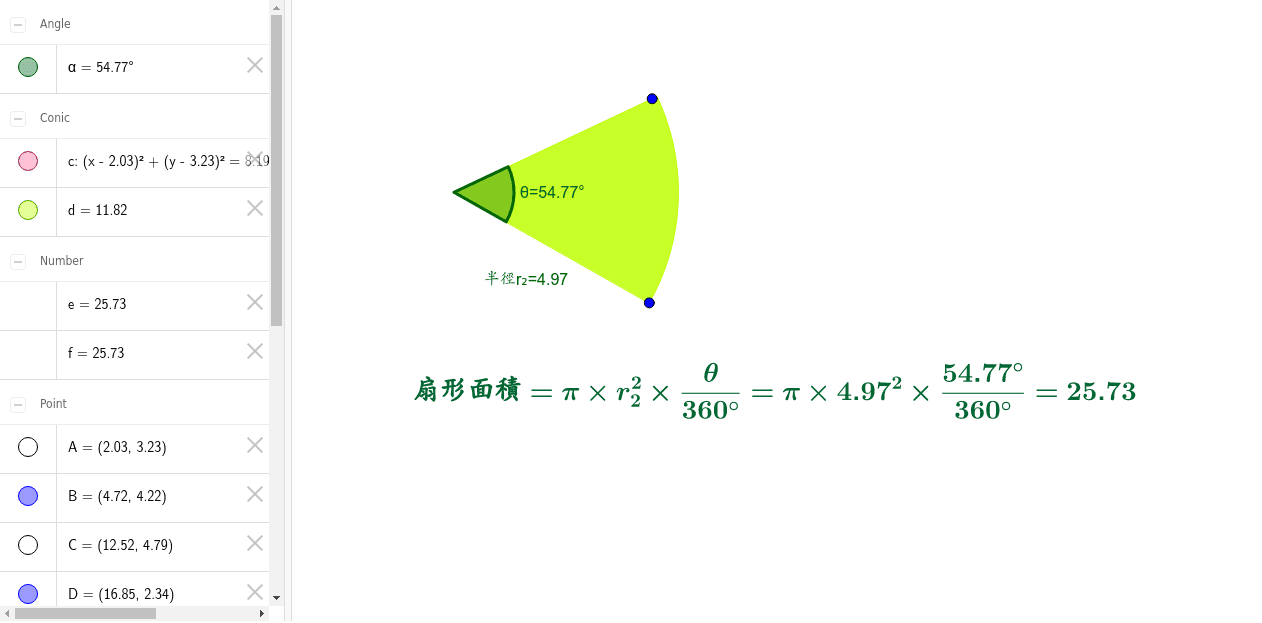



扇形面積 Geogebra
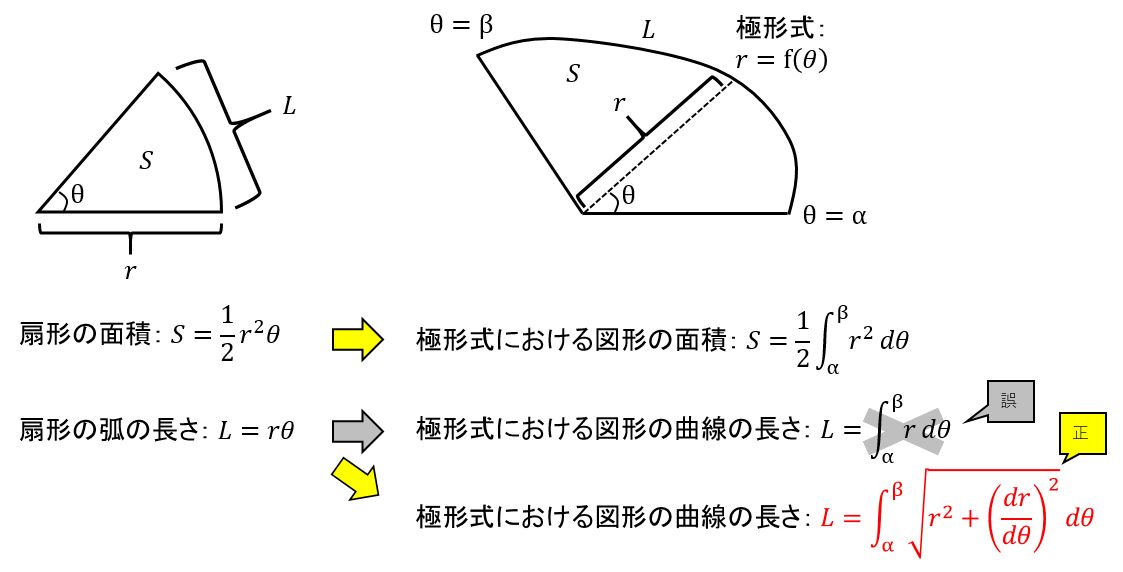



Lさんのツイート 今ミスしたことをまとめました 極形式について 面積は扇形から公式が作れるのですが 曲線の長さは扇形から作れません D 作れない理由は Rとr 2における近似レベルの違いな気がしますが 詳細は調べてません 数学 数検 高校




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




M Sudo S Room 楕円扇形の面積



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




扇 おうぎ 形の面積を求める公式と弧の長さの求め方



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe




圓的周長與面積 19 扇形的面積計算 Youtube
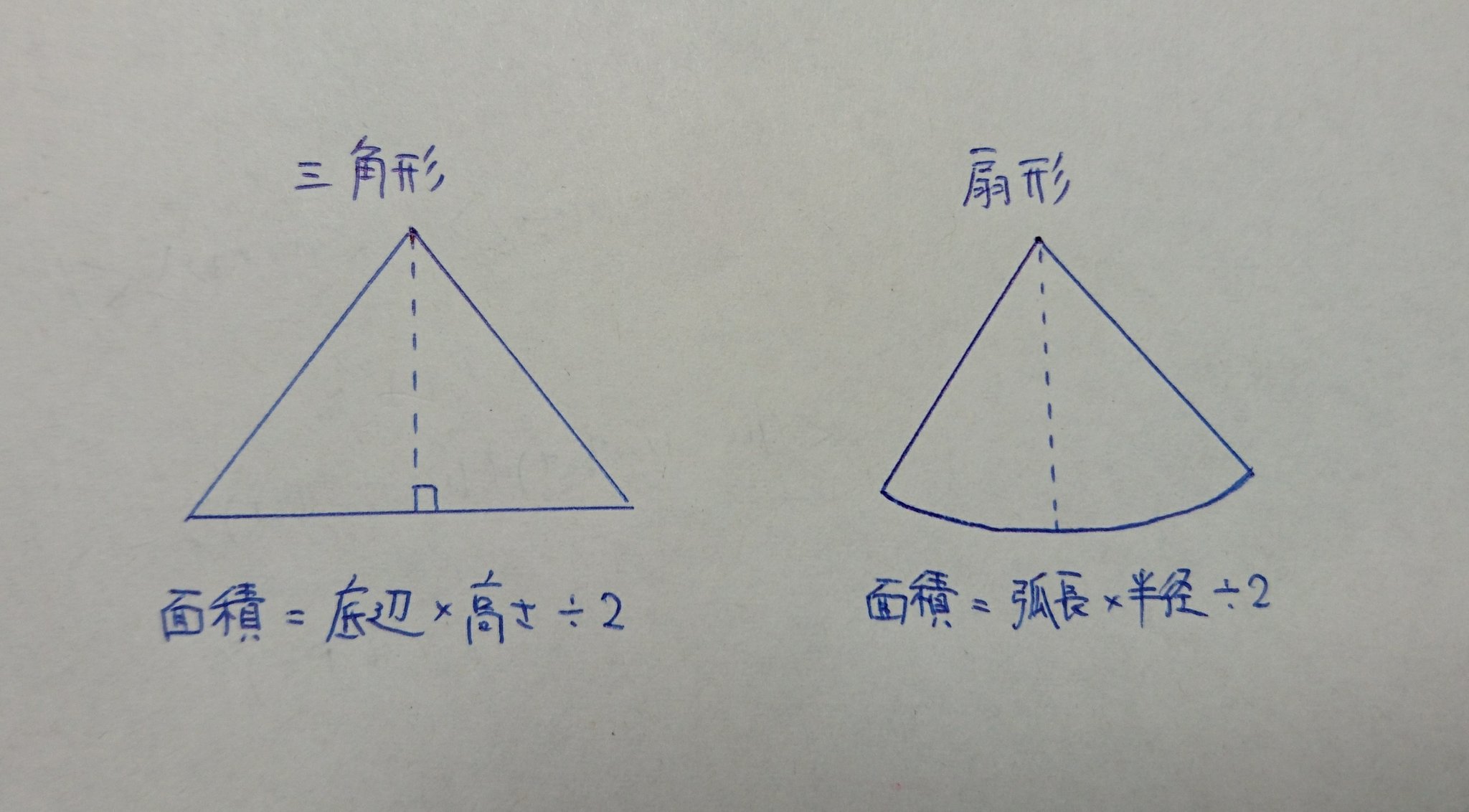



تويتر ヨビノリやす على تويتر センターのラジアンで思い出したんだけど 扇形の面積を求めるのに 扇形を三角形だと思い込んで 底辺 高さ 2 のように 弧長 半径 2 とすれば求められるのってみんな知ってる話 T Co Rgnzj006w3




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
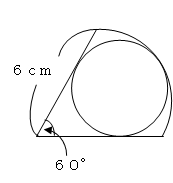



図形 扇形の面積から 扇形に内接する円の面積を引いた部分の面積を求める 子供に教える算数のツボ




正方形扇形面積 扇 おうぎ 形の面積を求める公式と弧の長さの求め方翻譯此網頁 Voajcr
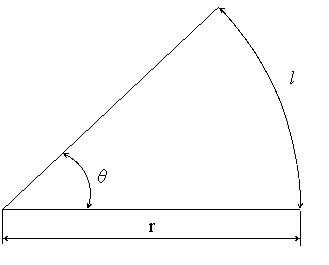



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ
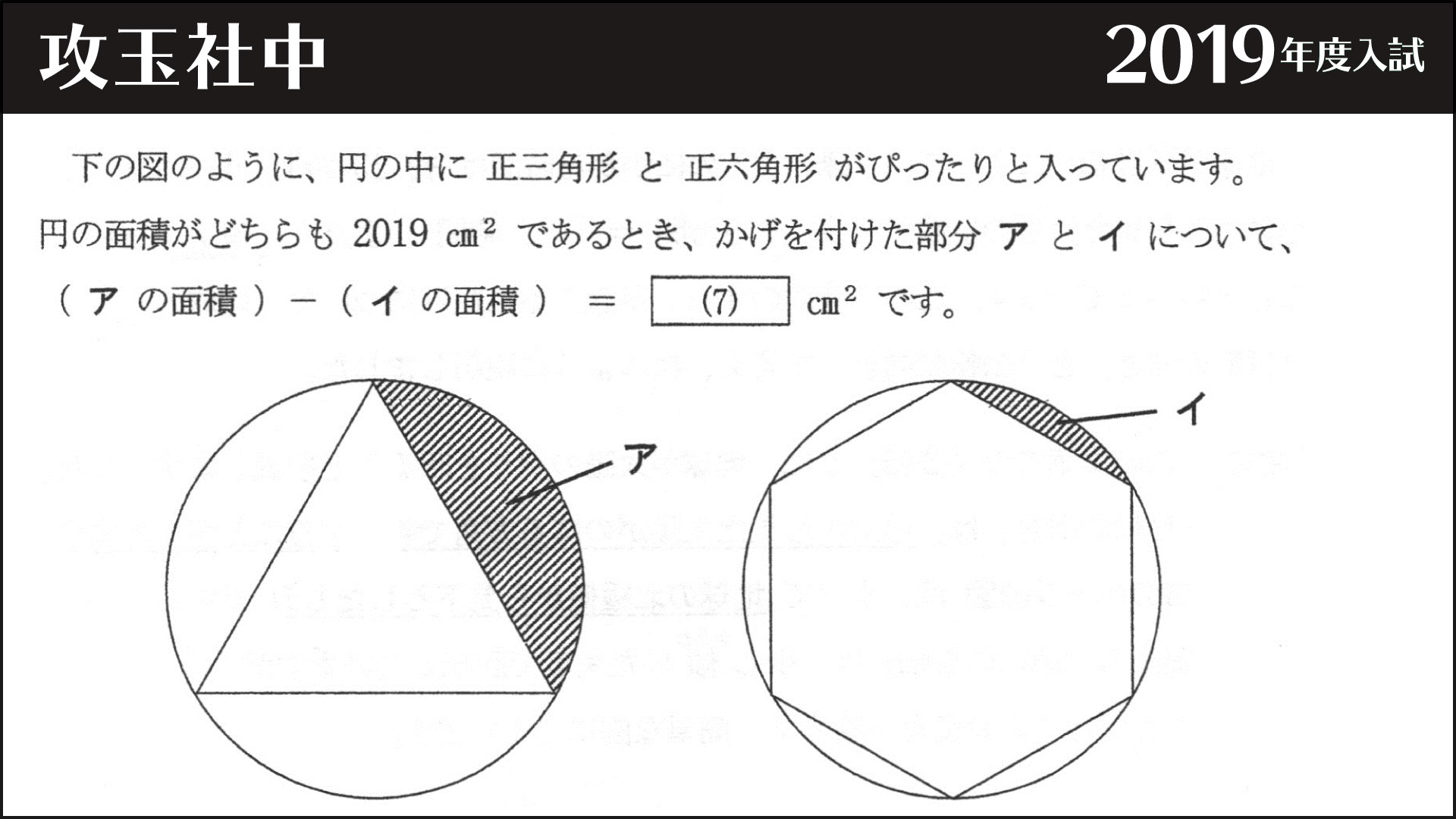



攻玉社 正六角形と正三角形と扇形の面積 ジーニアス 中学受験専門塾




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




扇形や円の問題と図形の回転移動 駒澤塾 中学受験の算数 理科




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




数ii 三角関数弧度法 弧の長さ 扇形の面積 Youtube




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月



求積問題 正方形と扇形




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear




高校受験の入試問題によく出る 扇の面積を使った応用問題 中学数学 By じょばんに マナペディア




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



0 件のコメント:
コメントを投稿